Understanding Crypto Pools
What is Crypto Pool?
Curve’s StableSwap concentrates most of the liquidity in the pool around the 1:1 exchange rate, providing much higher liquidity than CP-AMM(Constant-product Automated Market Maker) in stablecoin swaps. (More on this in our previous post.)
What if, we could apply this idea to asset pairs other than stablecoins?
Even volatile asset pairs do have periods with a steady price level. If we could provide concentrated liquidity during these periods, the swaps would be much more liquidity-efficient. Curve Finance’s Crypto Pool(a.k.a Curve v2) started with this idea and developed an algorithm that provides much more efficient liquidity for asset pairs other than stablecoins.
However, applying the StableSwap curve directly to other asset pairs will definitely pose some problems. StableSwap curve provides concentrated liquidity around the 1:1 exchange rate, but very weak liquidity beyond that range; so if the price fluctuates dramatically, it provides much lower liquidity than CP-AMM does. Moreover, liquidity providers would have to take on bigger impermanent losses, since the asset with higher value would also decrease dramatically. For these reasons, Crypto Pool proposes a different curve from that of StableSwap.
Crypto Pool needs to be constructed in a way that dynamically reacts to the market price, unlike StableSwap which focuses only around the 1:1 price. In this sense, Crypto Pool would need concentrated liquidity near-equilibrium price, but when the market price starts to deviate its curve should quickly resemble that of the CP-AMM. Its implementation as a formula will be elaborated in the next section.
Furthermore, we need an algorithm capable of dynamically shifting its “internal” equilibrium price to provide concentrated liquidity suited to real-time market conditions. Crypto Pool calls this process of adjusting the equilibrium price accordingly “repegging.” However, if repegging is conducted every time, it will create more losses for liquidity providers. So we need a special strategy to prevent such loss, which will be dealt with in the following section.
Crypto Pool Formula
Let’s call the balance of each asset in the pool x = (x₁, x₂).
The Crypto Pool contract internally keeps track of the equilibrium price p = (p₁, p₂) and is designed to provide concentrated liquidity around this price point.
First, let’s define x’ = (p₁x₁, p₂x₂) using x and p, because we need to derive a general form of equation regardless of p.
Now, the Crpyto Pool’s curve can be defined in a more general form: I(x’, D) = 0. D is the total value of the liquidity pool also defined as the sum of x' at the equilibrium (Equilibrium point is x’_eq = (D/2, D/2))
Now Crypto Pool curve’s equation (For convenience, we will use x instead of x' from now on):
KD(x₁ + x₂) + x₁ x₂ = KD² + (D/2)²
K is the same quantity represented by χ from StableSwap formula(Previous Post) which represents similarity to CS-AMM. K equals to 0 gives us CP-AMM and K diverging to infinity gives us CS-AMM. Remember, our curve needs to behave like StableSwap near the equilibrium point, but approach CP-AMM faster than StableSwap when moving away from it, meaning a faster reduction of K. Therefore we define K as :
K₀ = 4 x₁ x₂ / D²
K = AK₀ {γ² / (γ + 1 - K₀)²}
K₀ is basically χ from StableSwap(excluding the A), value of which is 1 when on the equilibrium point, but reduces to 0 farther away from the equilibrium. Each pool has its coefficient A just like in StableSwap, where bigger A implies similarity to the CS-AMM curve around the equilibrium point. γ is also different by the pool, where lower γ implies faster decay of K(=faster approach to CP-AMM curve) when moving away from the equilibrium point.
The below graph shows the relationship between K₀ and K for several γ’s(Note that we get the StableSwap formula when substituting K = AK₀).
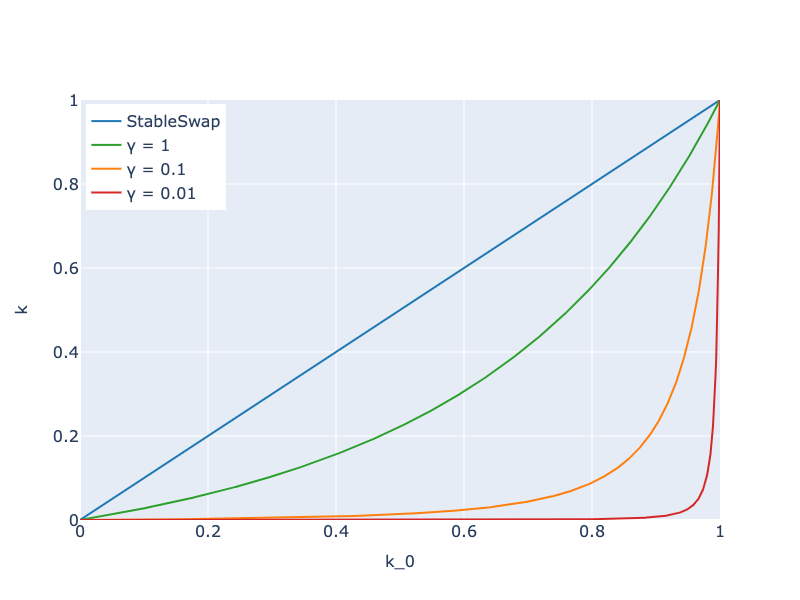
Crypto Pool is similar to StableSwap near the equilibrium point(K₀ = 1), but as we get away from the equilibrium(K₀ → 0), K decays at a faster rate than StableSwap does. This means Crypto Pool approaches CP-AMM at a much faster rate than StableSwap does when the price shifts away from the equilibrium price. Here γ controls the rate at which K is decaying(=rate at which Crypto Pool curve is approaching CP-AMM curve). Usually, we use γ of extremely small scale—below 0.0001.
The below graph compares the curves of Crypto Pool, CP-AMM, and StableSwap.
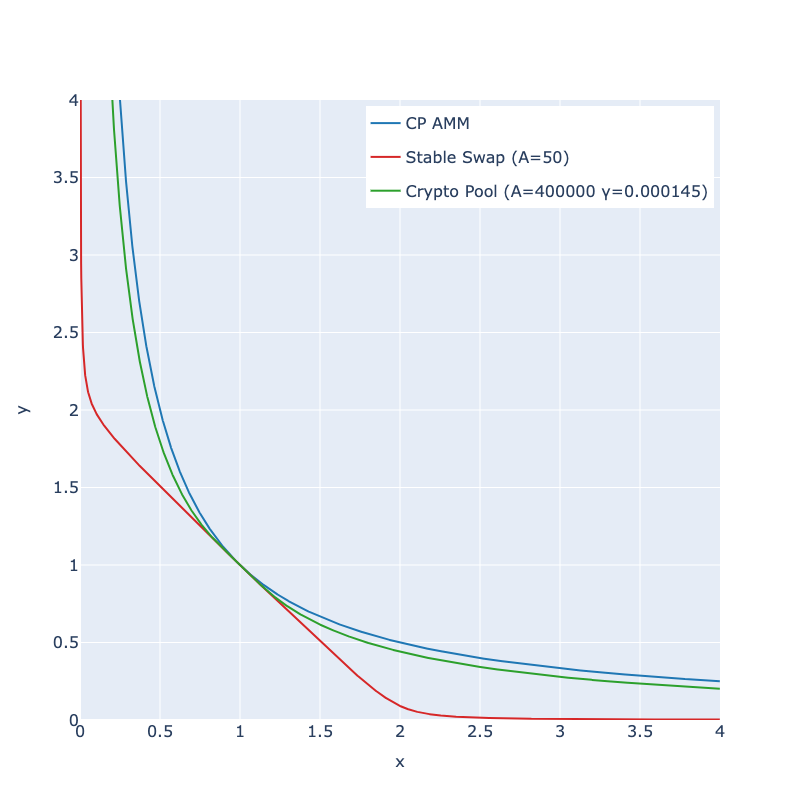
Crypto Pool provides a flat region only near the equilibrium point of (1,1), but quickly follows the shape of CP-AMM outside the equilibrium. Crypto Pool can be applied to asset groups with price volatility because it barely suffers from large impermanent loss of liquidity shortage, similar to StableSwap.
The below graph is the depth chart of asset x(assuming that asset y is a stablecoin and that equilibrium price is $1). “Depth” here represents the amount you can buy or sell(in USD) from $1 to a particular price point. It’s identical in meaning with the “depth chart” used in general order-book-based trading systems.
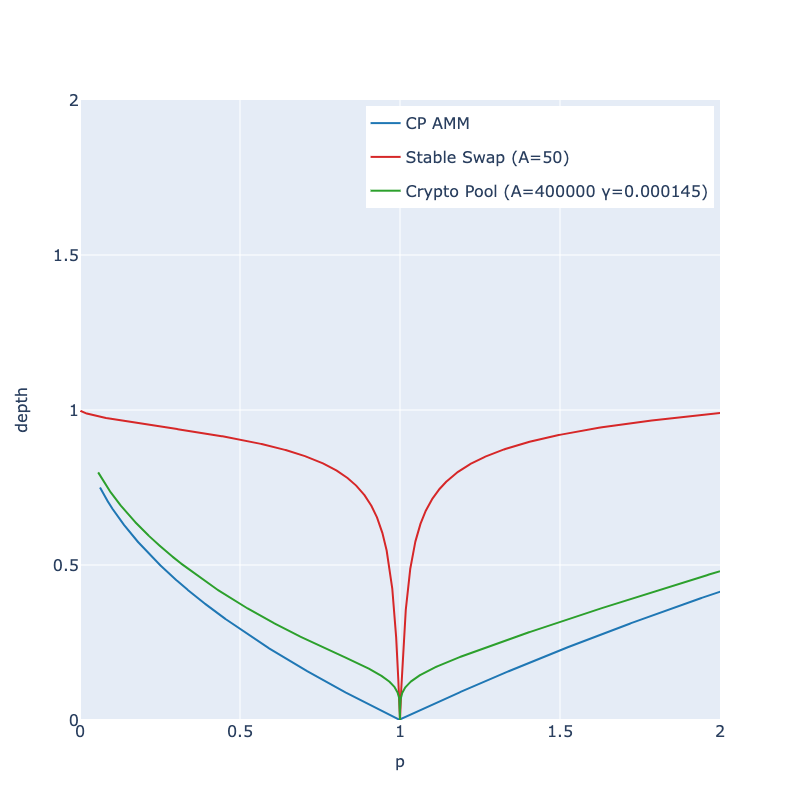
In Crypto Pool’s depth chart, more depth is guaranteed near the equilibrium than CP-AMM while also following the shape of CP-AMM depth outside the equilibrium. For 1% depth — the depth for 1% price change — comparison, Crypto Pool provides 19 times higher liquidity than CP-AMM and 5.3 times for 5% depth.
Following is the graph of dy / d(ln p) along p. This quantity represents the thickness of bid/ask orders in a typical order-book trading system.
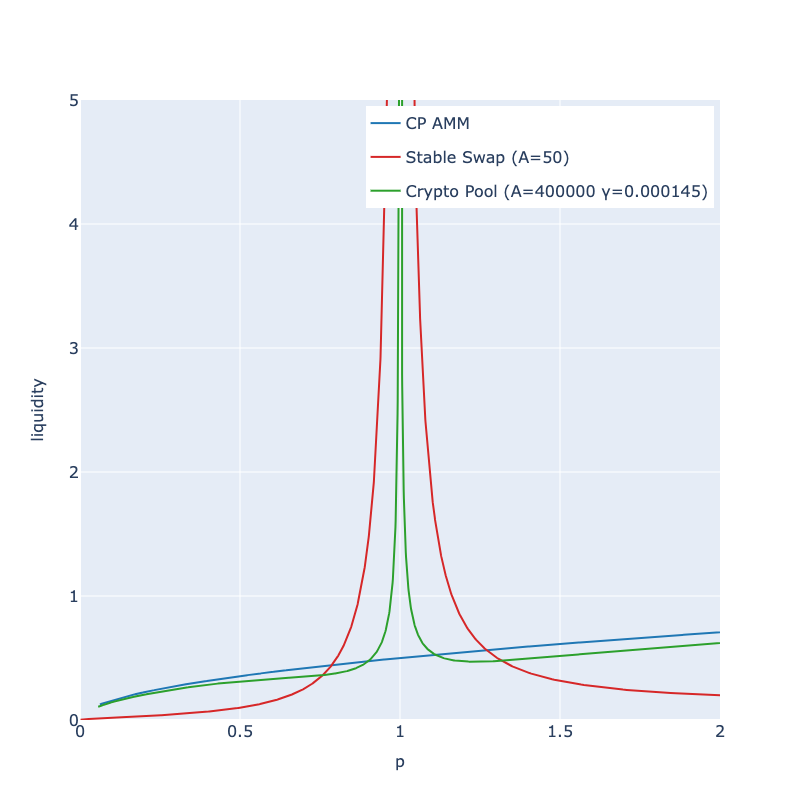
Crypto Pool provides much more concentrated liquidity near the center compared to CP-AMM but maintains similar liquidity to CP-AMM level outside the equilibrium. Thicker liquidity is formed around -11% ~ +11% range centered around the equilibrium price.
Repegging Algorithm
We have until now seen that Crypto Pool successfully concentrates liquidity around the equilibrium. However, one last problem remains: when the market price is way off the equilibrium price of the algorithm, Crypto Pool provides lower liquidity than CP-AMM. Thus, we need to repeg the equilibrium price with a certain strategy to concentrate liquidity at the right price at the right time.
The equilibrium price is basically determined through an internal oracle price using EMA(Exponential Moving Average). But too much repegging could cause additional loss for liquidity providers.
CP-AMM’s curve remains the same regardless of price movement, thus loss on the liquidity provider’s side can be recovered once the price recovers — thus called ”impermanent” loss. On the contrary, Crypto Pool is vulnerable to permanent loss(which cannot be recovered even if the price does) due to changes in the curve itself when repegging the equilibrium price.
To fully grasp what this means, let’s first imagine order-book-based market making. The market maker currently placed a $0.99 bid order and $1 ask order. Suddenly someone makes a huge buy and shifts the market price up to $1.2. The market maker — in order to market make — now places new $1.2 bid and $1.21 ask orders, canceling the previous ones. Once more, someone makes a huge sell and shifts the market price back to $1. Ultimately, the loss occurred on the market maker’s side for selling the asset at $1 and buying it again at $1.2. Had the market maker not instantly reacted to the spike in market price, this loss could’ve been prevented.
This example assumes only one of each bid and ask order, but the same logic applies with multiple orders across various prices. Crypto Pool can be thought of as market-making where orders are scattered across every price point, with some more orders specifically concentrated around the equilibrium price. If Crypto Pool does not conduct any repegging — if it maintains the same liquidity — spike in the market price wouldn’t have caused any losses for liquidity providers. But if Crypto Pool conducts repegging like the market maker above, the loss can occur because it sells at the lower price and rebuys at the higher price. So we can know that if Crypto Pool conducts repegging every time, a permanent loss can occur to liquidity providers.
To prevent such permanent loss for liquidity providers, Crypto Pool adjusts the equilibrium price only when specific conditions are met.
Before diving in, we need to quantify the potential loss(or gain) caused by repegging. To construct it, the Crypto Pool algorithm uses the invariant from the CP-AMM curve(D from xy = D²) at an equilibrium point. The result is as below:
X_cp = {(D²/(4p₁p₂)}^(1/2)
Crypto Pool’s contract internally keeps track of two variables: xcp_profit and virtual_price. xcp_profit represents the growth rate of xcp attributable to the accumulated fees and virtual_price represents the growth rate of xcp that additionally reflects repegging loss(or gains) on top of xcp_profit. In other words, virtual_price implies each token’s share value within the liquidity pool and xcp_profit implies each token’s share value is only added by pool’s fees.
Repegging only occurs when the following condition is expected to be satisfied: (virtual_price - 1) > (1/2) * (xcp_profit - 1). With this condition, Crypto Pool sets the lower bound over liquidity provider’s loss to half of the accumulated fee revenue.
Moreover, since the invariant from CP-AMM is used to quantify liquidity pool value, Crypto Pool’s liquidity provider has a limited range of possible loss similar to that of CP-AMM’s. Finally, Crypto Pool’s initial goals have been achieved: reducing the risk level similar to CP-AMM while also providing concentrated liquidity around the market price, both of which will ultimately attract higher revenue.
Conclusion
Summarizing the core logic into two bullet points:
Crypto Pool provides concentrated liquidity around the equilibrium price, but a similar amount of liquidity as CP-AMM beyond a certain range away from the equilibrium price.
The equilibrium price tracks the market price but is adjusted within a set boundary — half of the accumulated fees — to prevent the liquidity provider’s loss.
CP-AMM is logically simple in that it just provides relatively uniform liquidity for every price point from zero to infinity, but contains a critical flaw of wasting most of the liquidity, away from where most swaps occur. On the contrary, Crypto Pool concentrates liquidity only around the current equilibrium price, providing much richer liquidity at most times than CP-AMM. This would attract more users, leading to larger trading volumes and higher yields for liquidity providers.
Uniswap V3 also attempts to provide concentrated liquidity around the equilibrium price. There, liquidity providers can select a price range for which to provide liquidity. Thus, “overall concentrated liquidity” is achieved through active market participation of liquidity providers on where the liquidity should be focused. However, its drawbacks are clear in that liquidity providers not only need to understand the exact mechanism of this pool but also need to constantly monitor the market conditions as well as react to them. On the other hand, Crypto Pool doesn’t require actions on the liquidity provider’s side, making it suitable for the wider mass audience.
Moreover, Uniswap V3’s LP position cannot easily be integrated with other protocols, for they are not fungible — they are NFTs — due to the price range attached to each of them. This also makes it much harder to implement yield farming in the form of staking the fungible LP tokens. Sure enough, Crypto Pool need not consider these limitations at all, rendering it applicable throughout the whole DeFi ecosystem.
Last updated